负泊松比结构由于具有不同于普通结构的独特性质,在很多方面具备了其他结构所不能比拟的优势,如提高了结构的切变模量、抗缺口性能、抗断裂性能、承载能力以及弹性性能[1-2]。
目前对负泊松比结构特性[3]已经有较为广泛的研究。赵亚斌等[4-5]认为,由切变模量与泊松比的等式关系可知,当泊松比值为负时,杨氏模量与切变模量数值会非常接近,结构具有极高的可压缩性但却很难发生剪切。杨智春等[6]认为,传统结构在承受冲击载荷作用时,会在冲击力作用下发生压缩,并在垂直于冲击力的方向上从冲击部位向四周形变,而负泊松比结构在承受冲击载荷作用时,在冲击方向上承受压缩,而在侧面发生收缩,结构将向冲击部位形变,从而产生更大的抵抗压痕的作用。卢子兴等[7]通过研究得出:传统泡沫材料和负泊松比泡沫材料在拉伸时的断裂行为都显示出脆性材料的力学性能,由于负泊松比微结构比较复杂且不规则,因此其断裂韧性受体积压缩率的影响,在退火状态时,随着体积压缩率的增大其韧性成倍提高。上述研究主要是针对负泊松比结构的力学性能展开的,对于负泊松比结构本身的设计方法的研究较少。若直接以负泊松比为优化目标,采用拓扑优化方法使目标函数无限接近-1,则实现具有极限负泊松比属性的微结构优化是非常困难的[8]。基于一般的优化求解算法是很难实现的,必须额外添加约束或者改进优化求解算法[9]。国外学者Andreassen等[10-11]基于均匀化理论和能量法,直接以负泊松比为优化目标,以结构各向同性、材料用量为约束,同时额外增加了体积模量约束,求解得到了二维负泊松比拓扑构型,但对于OC(optimality criteria,最优准则)算法本身,其复杂程度大大提高。
本文基于能量法[12]、均匀化方法[13],结合拓扑优化理论[14-15],构建了一种可以求解负泊松比微结构拓扑构型的优化模型,既避免了以负泊松比为优化目标时会出现的高度非线性问题,也不需要额外增加约束条件导致算法复杂程度提高,并通过模拟仿真和实验测试方法来验证所构建优化模型的正确性。
1 负泊松比微结构拓扑优化模型的建立与求解 1.1 负泊松比微结构拓扑优化模型的建立若直接以负泊松比表达式(v=-E1122/E1111)为目标函数,在求解具有负泊松比特性的拓扑构型时,存在高度非线性问题,采用OC算法求解时,必须添加额外的约束条件,这样增大了求解的复杂度,不利于优化模型求解。为了解决此问题,可以将原表达式简化成一种线性的函数来近似地拟合原来的负泊松比[16],本文构建了一种可以求解得到负泊松比拓扑构型的目标函数:
| $ C={E_{1122}} - \alpha ({E_{1111}} + {E_{2222}}) $ | (1) |
该目标函数在结构形式上不存在高度非线性问题,式中:E1122为沿1方向拉伸时,沿2方向产生的能量;E1111为沿1方向拉伸时,沿1方向产生的能量;在各向同性材料中,为考虑数值的稳定性,这里引入沿2方向拉伸时沿2方向产生的能量E2222;α是初始值为0.8的常数。在采用OC算法求解时,随着迭代次数的增加,α以0.05的步长递减,当α接近0.001时迭代终止,此时沿1方向的能量E1111和沿2方向的能量E2222基本不变。目标函数可以表示为C=E1122,根据算法此时得到的目标函数值最小, 即E1122有最小值的同时,E1111保持不变,从而可将负泊松比表达式中的2个变量问题转化为单一变量问题。
本文的优化目标是:在满足约束条件下,得到结构负泊松比的最大绝对值(即极限负泊松比)。故本文构建的微结构拓扑优化数学模型为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{min}}}&{C={E_{1122}} - \alpha \left( {{E_{1111}} + {E_{2222}}} \right)}\\ {{\rm{s}}{\rm{.t}}{\rm{.}}}&{V\left( x \right) \le f{V_0}0}\\ {}&0<{x_{\rm{min}} \le x \le 1} \end{array}} \right. $ | (2) |
式中:V(x)为材料体积,x为设计变量;f为体积比;V0为设计域体积;为避免在优化过程中单元刚度矩阵出现奇异,取xmin=0.001。
1.2 负泊松比微结构拓扑优化模型的求解由Xia Liang、张卫红等[16-17]提出的能量法,得到等效弹性系数矩阵DH:
| $ {\mathit{\boldsymbol{D}}^H}=\left[ {\begin{array}{*{20}{c}} {2{E^{(1)}}}&{{E^{(4)}} - {E^{(2)}} - {E^{(1)}}}&0\\ {}&{2{E^{(2)}}}&0\\ {{\rm{sym}}}&{}&{2{E^{(3)}}} \end{array}} \right] $ | (3) |
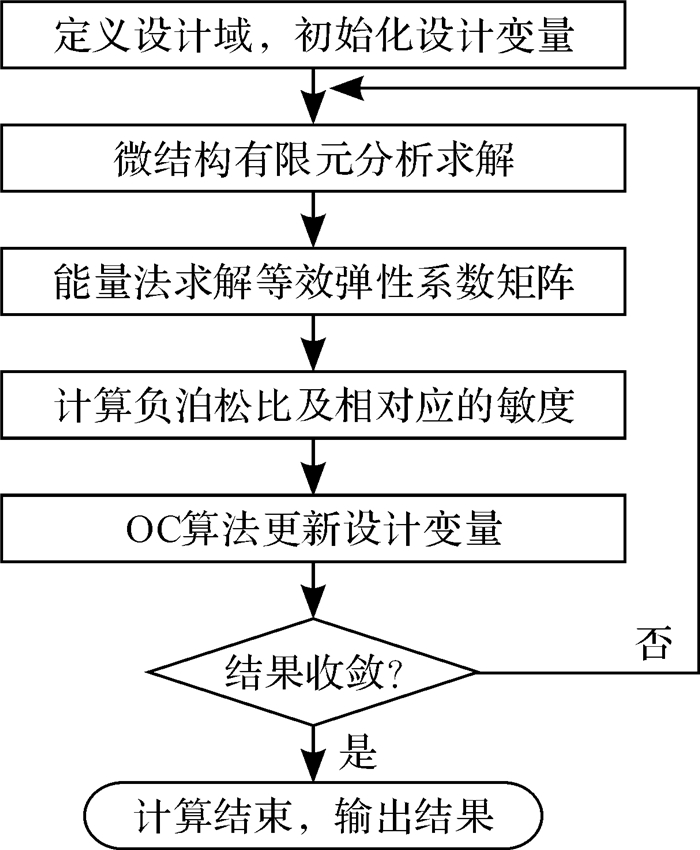
结合有限元分析,采用OC算法即可对上述优化模型进行优化求解,优化流程如图 1所示。
|
| 图 1 负泊松比微结构拓扑优化流程 Fig.1 Flow of topology optimization design for negative Poisson's ratio microstructures |
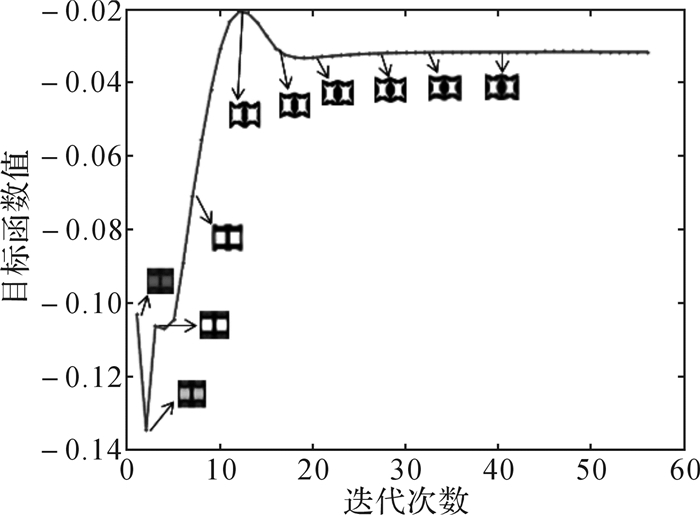
给定的数值算例的微结构设计域如表 1所示,材料的弹性模量E0=2.1×105 N/mm2,泊松比μ=0.3。将体积约束设为f=0.5,离散成100×100个单元。参考文献[18]的方法,从整体结构考虑,本文采用敏度过滤的方法,以保证单胞间的连通性,得到微结构最优拓扑构型,选取3种单胞组合形式,具体结果如表 1,表中构型图中黑色表示实体材料部分,白色表示孔洞部分。3种宏观结构在本质上与微结构无区别,可直观地表达微结构构型。图 2所示为目标函数优化过程的迭代曲线。
| 设计域 | 最优拓扑构型 | 等效弹性系数矩阵 | 负泊松比 | ||
| 单胞1×1 | 单胞2×2 | 单胞3×3 | |||
 |
 |
 |
 |
v1=-0.41 | |
|
| 图 2 目标函数优化过程的迭代曲线 Fig.2 The iterative curve of objective function in the optimization |
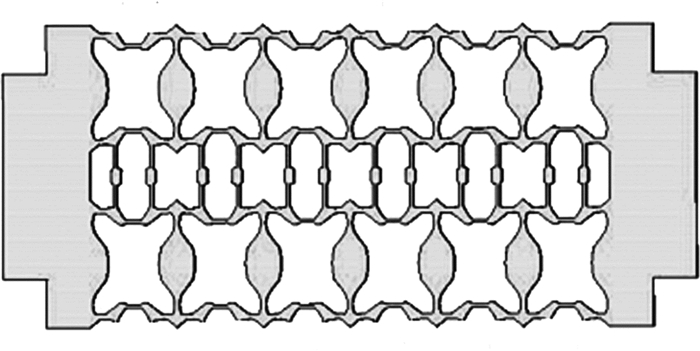
为了验证数值模型和数值算例的正确性,采用静力学仿真与动力学仿真来模拟试样拉胀过程,仿真模型的物性参数与数值算例相同,并将仿真后得到的负泊松比与优化模型求解得到的极限负泊松比进行对比分析。图 3为对单胞2×2形貌重构后的几何模型。
|
| 图 3 单胞2×2几何模型 Fig.3 The geometrical model of the base cell 2×2 |
对图 3几何模型添加约束条件,在左右横截面的Y方向均施加固定约束,考虑试样的弹性变形,左横截面X方向施加位移x=-0.1 mm,右横截面X方向施加位移x=0.1 mm。其位移约束如图 4所示。

|
| 图 4 试样位移约束仿真图 Fig.4 Displacement constraints simulation diagram of the sample |
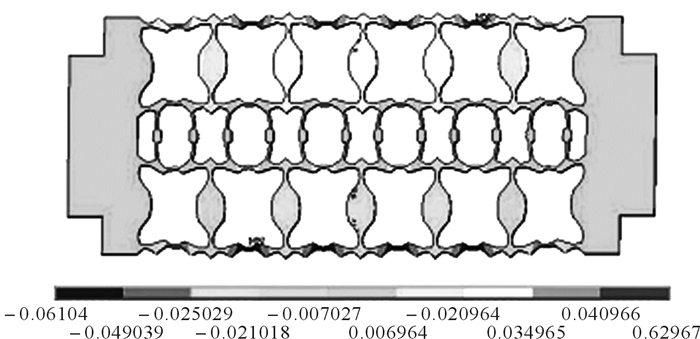
在有限元软件中求解后,试样结构变形如图 5,试样沿Y方向的位移云图如图 6。

|
| 图 5 试样结构变形的静力学仿真图 Fig.5 The statics simulation diagram of sample structure deformation |
|
| 图 6 试样沿Y方向位移的静力学仿真云图 Fig.6 The statics simulation diagram of sample displacement along Y direction |
由图 5可知,试样具有负泊松比拉胀特性。由图 6可得,在左右边界面上各施加沿X方向0.1 mm位移约束时, 试样在Y方向上的整体平均变形为0.49 mm, 由泊松比定义:
| $ {{v'}_1}=- \frac{{横向应变变化量}}{{轴向应变变化量}} $ | (4) |
得
所求解的负泊松比值v′1与优化模型求解得到的负泊松比值v1的绝对值差仅为0.08,通过试样静力学仿真分析验证了所构建优化模型的正确性。
3.2 动力学仿真分析动态法测试试样的负泊松比是在有限元软件中模拟机械式测试法求解试样负泊松比,通过模拟试样加载的整个过程,记录试样由初始的拉胀至后来的拉缩的整个过程的横向变形变化与轴向变形变化,并绘制横向变形-轴向变形曲线。动态分析法较静态分析法更加直观,数据更加充足。
对试样进行动力学仿真分析,仿真过程如图 7所示。
|
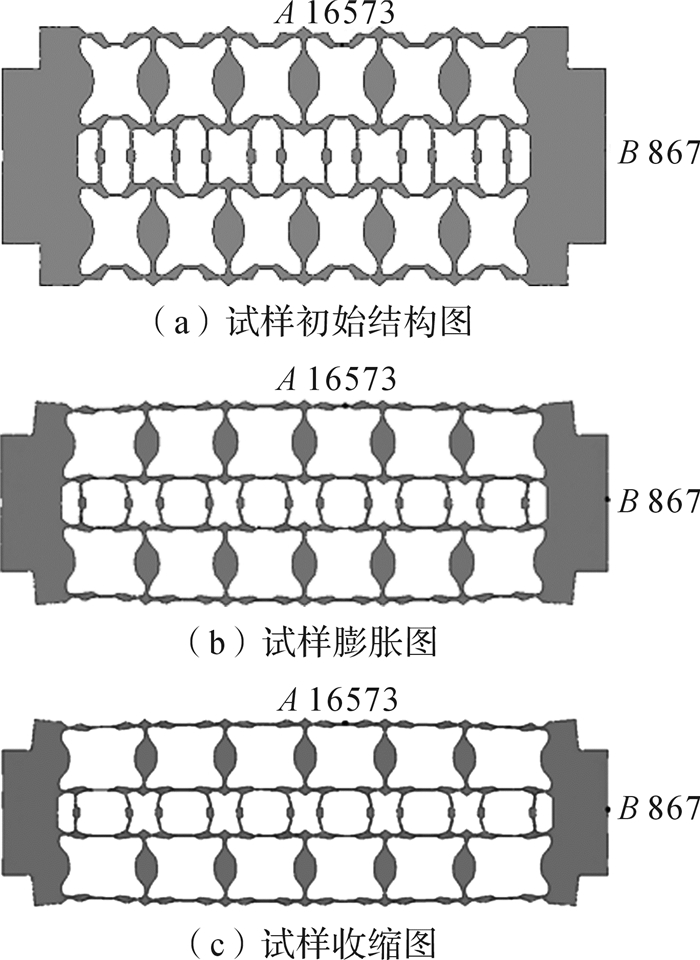
| 图 7 动力学仿真过程中的试样结构图 Fig.7 Sample structure diagram during dynamics simulation process |
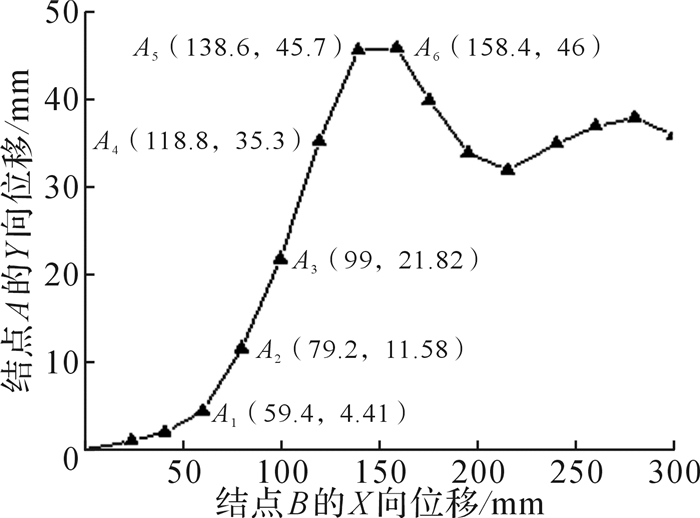
由图 7中(a)、(b)、(c)可知,试样在动力学仿真过程中经历了先拉胀再收缩的过程。由静力学仿真分析可知,试样中心节点A(编号为16573)的拉胀性能最好,即它沿Y方向位移最大,故在探讨试样拉胀位移时以结点A为研究对象; 根据施加的位移约束,任取轴向截面上的结点B(编号为867)为研究对象。在动力学仿真的过程中,以结点A的Y方向位移为纵坐标,结点B的X方向位移为横坐标自动生成位移曲线, 如图 8所示。
|
| 图 8 结点A,B的位移曲线 Fig.8 Displacement curve of the node A, B |
由图 8可知,在结点B沿X方向匀速移动时,结点A由静止开始缓慢沿Y方向运动,在到达A1位置时,其运动速度明显加快且在A6位置时拉胀至最高点(即试样在弹性范围内允许到达的最大膨胀位移)。随着结点B继续沿X向移动,结点A开始慢慢回缩。为了研究试样的拉胀特性,取结点A沿Y方向的A1至A6位移段分析。所求解的负泊松比为:
| $ {{v''}_1}=- \frac{{横向位移变化量}}{{轴向位移变化量}}=- \frac{{158.4 - 59.4}}{{46 - 4.41}}=- 0.42 $ | (5) |
所求得的负泊松比值v″1与优化模型求解得到的负泊松比值v1=-0.41的绝对值差仅为0.01,在误差允许范围内。通过试样动力学仿真分析有效证明了上述所构建优化模型的正确性。
4 试样负泊松比的实验测试 4.1 实验原理参考国家标准GB/T 22315—2008《金属材料弹性模量和泊松比试验方法》[19],通过实验记录样品的横向变形与轴向变形,绘制横向变形—轴向变形曲线,在记录的横向变形—轴向变形曲线上,选取合适的数据,确定弹性直线段,在该弹性直线上选取尽量远的相邻两点之间的横向变形变化量和轴向变形变化量,即可计算得到试样负泊松比值。
4.2 实验样品及实验器材实验样品几何结构与模拟几何模型相同,选取201拉丝不锈钢为原材料,采用激光加工而得。实验样品如图 9所示。

|
| 图 9 实验样品 Fig.9 The experimental sample |
实验器材如下:万能拉伸试验机,按国家标准GB/T16825.1进行检验,其准确度应为1级或优于1级,液晶显示主要内容有试验力、位移、峰值、运行状态、运行速度等;引伸计,最小刻度值为0.001 mm,指针旋转1圈为0.2 mm,表盘上显示量程为0~1 mm;表座,测量时固定在引伸计上;托盘和三角支架,用于支撑表座,三角支架可以上下调节。实验装置如图 10所示。

|
| 图 10 实验装置图 Fig.10 The experimental device diagram |
1) 标记测试点。如图 9所示,在测试点位置上分别做好标记“1-1”“1-2”“1-3”。
2) 调零。旋转引伸计表盘,使表盘指针指向“0”刻度。
3) 实验测试。在万能拉伸试验机显示屏上设置,使夹具以1 mm/min的速度缓慢向下运行,引伸计表盘指针开始摆动, 待其指针稳定后,立即暂停加载,分别读取引伸计上的示数即为试样的横向膨胀位移,显示屏上夹具的行程即为试样的轴向拉伸位移。为了使试样在每次实验中均可实现弹性变形,试样的轴向拉伸位移均不超过3 mm,故每测试5组数据后就必须对试样进行卸载,然后重复上述实验。
4) 绘制变形曲线。记录数据并对测试数据进行合理分析,绘制横向变形—轴向变形曲线。
4.4 数据处理与分析测得的试样数据如表 2所示。将此数据绘制成横向变形-纵向变形曲线,其中横坐标表示试样的膨胀位移,纵坐标表示试样的拉伸位移, 如图 11所示。
| mm | ||||||
| 测试点 | 初始坐标 | 随载荷变化的结点坐标 | 最终坐标 | |||
| 1-1 | (0, 0) | (0.088, 0.892) | (0.242, 1.072) | (0.47, 1.684) | (0.55, 1.884) | (0.67, 2.77) |
| 1-2 | (0, 0) | (0.11, 0.307) | (0.28, 0.579) | (0.41, 0.84) | (0.56, 1.27) | (0.823, 2.01) |
| 1-3 | (0, 0) | (0.164, 0.216) | (0.44, 0.55) | (0.662, 0.983) | (0.674, 1.016) | (0.91, 2.54) |
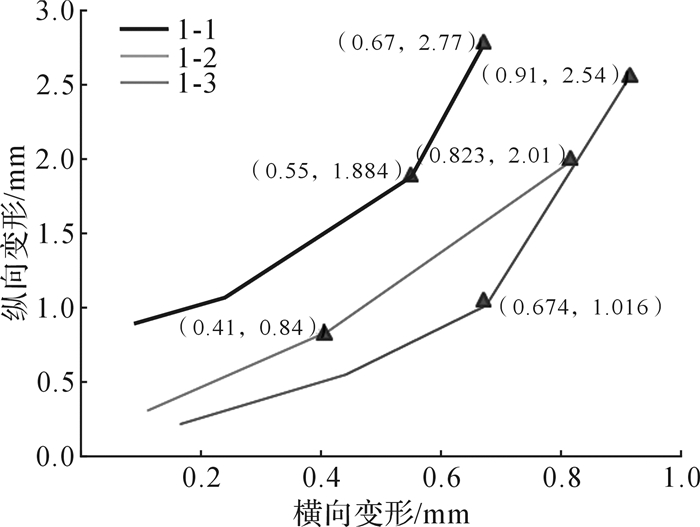
从图 11可知,所绘制的3条曲线均为直线段,说明试样在纵向加载过程中,均处于弹性范围内。
|
| 图 11 试样横向变形—纵向变形曲线 Fig.11 The transverse deformation—longitudinal deformation curve of sample |
对比3个测试点的数据曲线,测试标记为“1-2”的曲线的数据基本在同一直线,相比其他两条曲线来说更为稳定,参考国家标准GB/T22315—2008《金属材料弹性模量和泊松比试验方法》,选取直线上尽量远的相邻两点进行泊松比计算,故选取图 11中所标识的(0.823,2.01)mm和(0.41,0.84)mm两点。根据泊松比定义,该两点的横向变形变化量和相应的轴向变形变化量的比值即为所求泊松比:
| $ {{v'''}_1}=- \frac{{0.823 - 0.41}}{{2.01 - 0.84}}=- 0.353 $ | (6) |
尽管此实验受到了客观条件的限制,如在AutoCAD中重构试样不够精准、激光加工样品精度不高、引伸计针头灵敏度不够等因素都会引起实验误差,但实验测试求得的负泊松比值
本文构建了一种可以求解负泊松比微结构拓扑构型的优化模型,并在初始条件下计算得到相应拓扑构型和负泊松比。先后采用仿真分析和实验测试两种方法来测试拓扑构型的泊松比值。与优化模型求解得到的泊松比值对比,验证了所构建优化模型的正确性,为负泊松比结构的优化设计提供了一定的参考价值。



